Ecuaciones Trigonometricas

Bienvenidos nuevamente a este tutorial presentado por resolviendo.co para aclarar dudas sobre ecuaciones trigonometrícas.

Comentar Procedimiento.

Procedimiento Para Hallar la Inversa de Una Matriz

Bienvenidos Lectores en esta ocasion daremos unos tips para tener en cuanta el momento de hallar la Inversa de una Matriz, mostramos pasos fundamentales para que la metodologia sea eficiente para resolver.

Procedimiento

1. Se escribe la Matriz Aumentada [A | I ]

2. Se utiliza la reducción por renglones para poner la matriz A en su forma escalonada reducida por renglones.

3. Se determina si A es invertible

• Si la forma escalonada reducida por renglones de A es la Matriz Identidad I, entonces A^-1 es la Matriz que se tiene a la derecha de la Barra vertical.
• Si la Reducción de  A conduce a un renglón de ceros a la Izquierda de la Barra vertical, entonces A no es invertible. 

Para aclarar mas el Tema vamos a exponer un Ejemplo:

1. Hallar la Inversa de A

Solución

Escribimos la Matriz aumentada [A | I] y la Llevamos a la forma escalonada reducida:

Vamos Eliminando Dividimos la F1/3, F2/2 y la F3 la dejamos quieta y el resultado es el siguiente:

 

Ahora Multiplicamos la F3 por 1/3 y Sumamos la F1, y a su vez F3 le sumamos F2, y F3 la Multiplicamos por -1 y nos da el siguiente resultado:

 

Ahora nos falta eliminar el 2/3 de la F1 entonces realizamos lo siguiente -2/3F2 + F1 y nos queda los siguiente:

La Inversa de A es la Matriz que queda a la derecha en el desarrollo anterior, es:

 

Esta es la Solucion al Ejemplo Planteado

Dudas dejar comentario.

 

 

Biografía de Aristóteles (- 384 a - 322)

Aristóteles nació en Estagira, en Tracia, el año 384-3 a. C., según Diógenes Laercio, quien nos dice que era hijo de Nicómaco y Efestiada, y que su padre ejercía la medicina en la corte del rey Amintas (II) de Macedonia, "por causa de la medicina y por amistad", lo que se ha tratado de asociar con el posterior interés naturalista de Aristóteles. Diógenes Laercio nos describe a Aristóteles como "el discípulo más legítimo de Platón, y de voz balbuciente... que tenía las piernas delgadas y los ojos pequeños, que usaba vestidos preciosos y anillos, y que se cortaba la barba y el pelo". (Vidas de filósofos ilustres, libro V, 1).

Aristóteles en la Academia

Poco sabemos de la educación recibida por Aristóteles en su juventud, aunque debió ser la propia de los jóvenes griegos de su época. A los diecisiete años, el 368 a. C., se trasladó a Atenas donde se incorporó a la Academia de Platón en la que permanecería durante veinte años. A pesar de algunas anécdotas que se hacen eco de un supuesto enfrentamiento entre Platón y Aristóteles, antes de la muerte de aquél, es poco probable que tal enfrentamiento haya podido producirse, dado que todas las referencias que tenemos de Aristóteles hacia Platón hacen gala de un gran respeto y admiración hacia el maestro, pese a las discrepancias teóricas que luego llevaron a su separación doctrinal. El hecho de que la crítica contemporánea haya puesto de manifiesto el carácter histórico, evolutivo, de la obra aristotélica hace aún más insostenible dicha hipótesis. Sabemos que Aristóteles atravesó por una fase profundamente platónica antes de desarrollar sus propias concepciones filosóficas, asumiendo como propia, por ejemplo, la teoría de las Ideas de Platón, antes de haber procedido a su crítica, como claramente se pone de manifiesto en el diálogo aristotélico "Eudemo", una de sus obras de juventud.

A la muerte de Platón, en el - 347, Espeusipo, sobrino de Platón, se hizo cargo de la dirección de la Academia, bien por designación directa de éste o bien por decisión de sus condiscípulos, imprimiendo una orientación de carácter más especulativo y místico-religioso a las actividades de la Academia, lo que no fue del agrado de Aristóteles quien la abandonó, (ya fuera por esta razón, ya por sentirse frustrado al no haber sido designado él mismo como director, como sostienen otros.

Aristóteles tras el abandono de la Academia

Aristóteles se dirigió entonces, en compañía de Jenócrates, a Assos, donde reinaba el tirano Hermias, (con quien, al parecer, entabló profunda amistad), fundando allí una sección de la Academia que él mismo dirigió durante tres años. Fue allí probablemente donde comenzó a desarrollar sus propias opiniones contrarias a la teoría de las Ideas. De esta época es, en efecto, su obra "Sobre la filosofía", en la que aparecen los primeros elementos críticos de la teoría de las Ideas. También allí contrajo matrimonio con Pythia, hija adoptiva o sobrina de Hermias, con la que llevó una vida feliz hasta la muerte de ésta. (Desconocemos cuando tuvo lugar este acontecimiento, pero sabemos que Aristóteles tras la muerte de Pythia vivió con Herpilis, con la que tuvo un hijo llamado Nicómaco.)

Tres años después, en el 345-4, se trasladó a Mitilene, en la isla de Lesbos, entrando allí probablemente en relación con Teofrasto, que sería posteriormente el más destacado discípulo y continuador de la obra de Aristóteles. Allí continuó con su actividad filosófica hasta que en el año 343-2 fue llamado por Filipo de Macedonia para hacerse cargo de la educación de su hijo Alejandro, el futuro Alejandro Magno, que tenía entonces trece años. Probablemente dicho encargo se debiera más a la amistad y parentesco con Hermias, aliado de Filipo, y asesinado hacía poco mediante una trampa tendida por los persas, que al pasado de su familia en la corte de Macedonia. Allí permaneció siete u ocho años, hasta el 336-5, cuando Alejandro subió al trono, regresando entonces Aristóteles a Atenas.

Regreso a Atenas y creación del Liceo

Una vez en Atenas, en el 335, fundará su propia escuela, el Liceo, una comunidad filosófica al estilo de la platónica , llamada así por estar situada dentro de un recinto dedicado a Apolo Likeios. Además del propio edificio contaba con un jardín y un paseo (perípatos) del que los aristotélicos recibirán el nombre de peripatéticos, ya sea porque Aristóteles impartiera sus enseñanzas paseando, como recoge Diógenes Laercio ("... tomó en el Liceo un sitio para pasear, y paseando allí hasta la hora de ungirse los atletas, filosofaba con sus discípulos, y de este paseo fue llamado peripatético"), o porque, simplemente, se impartieran dichas enseñanzas en el paseo. (Excavaciones realizadas a mediados de los 90 en Atenas, cerca de la la Plaza Sintagma, dejaron al descubierto los cimientos de varios edificios, como se puede observar en la imagen, que los arqueólogos consideran pueden ser los restos del Liceo de Aristóteles). Según la tradición el orden de las actividades en el Liceo estaba fuertemente establecido, dedicándose las mañanas a las cuestiones más difíciles de carácter filosófico, reservadas para los discípulos, y las tardes a las lecciones de retórica y de dialéctica, entre las que se podía encontrar un público más amplio. 

A lo largo de este período Alejandro Magno realiza sus campañas militares que tienen como una de sus consecuencias la unificación de la Hélade, con la consiguiente pérdida de autonomía política de las ciudades estado, entre las que se contaba Atenas. El hecho de que Aristóteles hubiera sido su preceptor, así como su amistad y parentesco con Hermias, le irá convirtiendo en un personaje no grato para muchos atenienses. A la muerte de Alejandro, en el año 323, sintiéndose amenazado por los crecientes sentimientos antimacedónicos, Aristóteles abandonará Atenas y se retirará a Calcis, ("para que los atenienses no vuelvan a pecar contra la filosofía", dicen que dijo, en clara referencia a la condena de Sócrates), a una propiedad de su difunta madre, en la isla de Eubea, de donde era originaria. Allí morirá Aristóteles, el 322 a. C., de una enfermedad del estómago.

Fuente: webdianoia.com

Explicacion de Antiderivada o Integral

Bienvenidos Lectores en esta ocasion presentamos un video tutorial sobre antiderivadas cualquier ejercicio que tenga dudas enviar via email y con gusto le daremos la respectiva solucion y explicacion del proceso y tips para resolver o coger agilidad en la solucion.

Matriz Inversa en Algebrator

Bienvenidos lectores a este tutorial de solucion de una matriz 2x2 y 3x3 en el software algebrator presentado en ingles. Podemos observar el Procedimiento de dicho problema planteado mas su explicacion.

Nota: Realizaremos un Video en Español para que visualicen el procedimiento Textual.

Espacio Euclidiano N Dimensional

Lectores Bienvenidos a esta gran explicacion sobre espacio euclidiano es un tema interesante sobre vectores en un espacion dimensional.

Vectores en el Espacio Dimensional

Si n es un entero positivo, entonces una n-ada ordenadas es una sucesion de n numeros reales (a1, a2....,an) el conjunto de todas las n-adas ordenadas se denomina espacio n dimensional y se denota por R^n.

Dos Vectores U = (U1, U2.....Un) y V = (V1, V2.....Vn) en R^n se denominan iguales si:

U1 = V1, U2 = V2,......Un = Vn

La suma U + V Se define por:

U + V = (U1 + V1, U2 + V2)

Sea K un escalar, entonces el multiplo escalar KU se define por:

KU = (Ku1, Ku2, Kun)

Las operaciones de adicion y multiplicacion escalar en esa definicion se denominan operaciones nominales sobre R^n.

El Vector cero en R^n se denota por 0 y se define como el Vector.

0 = (0,0,0,......,0)

Si U = (U1, U2, U3,.....Un) es cualquier vector en R^n entonces el negativo o inverso aditivo de U se denota por -U y se define por:

-U = (-U1, -U2, -U3,......Un)

La diferencia de Vectores en R^n se define por:

U-V = (U1 - V1, U2 - V2,.......Un - Vn)

EJERCICIO

Si U = ( -3, 2, 1, 0),    V = (4, 7, -3, 2) y W = (5, -2, 8, 1). Hallar X que satisface 5X - 3V = 2(3W - 5X)

SOLUCION

5X - 3V = 6W - 10X 

5X + 10X = 6W + 3V 

15X = 6W + 3V

6W = (30, -12, 48, 6;)                                   3V = (12, 21, -9, 6)

15X = (30, -12, 48, 6) + (12, 21, -9, 6)

Realizamos la Operacion Matematica

15X =  (42, 9, 39, 12)

Despejamos X

X = (42/15, 9/15, 39/15, 12/15) Rpta

 

Biografía Platón

Filósofo griego (Posiblemente Nace cerca de Atenas en 427 - y muere el año 347 a. C.))

"El hombre sabio querrá estar siempre con quién sea mejor que él"
Platón

Platón se llamaba en realidad Aristocles. Recibió el apelativo con el que le conocemos y que significa ""espalda ancha" por su corpulencia. Durante su juventud llegó a ser bicampeón olímpico de lucha. Pertenecía a una familia noble. Su padre, Aristón, se decía descendiente del rey Codro, el último rey de Atenas. Su madre Períctiona, descendía de la familia de Solón, el antiguo legislador griego. Era además hermana de Cármides y prima de Critias. Platón tuvo dos hermanos, Glaucón y Adimanto, y una hermana, Potone. Tuvo una educación esmerada en todos los ámbitos del conocimiento. De joven, Platón tuvo ambiciones políticas pero se desilusionó con los gobernantes de Atenas. Es posible que se iniciara en la filosofía con las enseñanzas del heracliteano Cratilo. Cuando cuenta veinte años tiene lugar el encuentro con Sócrates que contaba entonces 63 años y se convertirá en su único maestro hasta su muerte. Proclamado discípulo de Sócrates, aceptó su filosofía y su forma dialéctica de debate: la obtención de la verdad mediante preguntas. Parece ser que fue testigo de la muerte de su maestro. Temiendo por su vida, abandonó Atenas algún tiempo y viajó a Italia, Sicilia y Egipto. En el año 387 Platón fundó en Atenas la Academia, institución a menudo considerada como la primera universidad europea. Se daban materias como astronomía, biología, matemáticas, teoría política y filosofía. Aristóteles fue su alumno más destacado. Ante la posibilidad de conjugar la filosofía y la práctica política, viajó a Sicilia en el año 367 a.C. para ser tutor del nuevo gobernante de Siracusa Dionisio el Joven. El experimento fracasó. Platón regresó a Siracusa en el año 361 a.C., pero una vez más su participación en los acontecimientos sicilianos tuvo poco éxito. Pasó los últimos años de su vida dando conferencias en la Academia y escribiendo. Murió próximo a los 80 años en Atenas en el año 348 o 347 a.C. Es el primer pensador griego cuya obra se ha conservado íntegramente, y Aristóteles ha transmitido incluso fragmentos de su enseñanza oral en la Academia, al parecer discordante con sus escritos. Sus escritos adoptaban la forma de diálogos, exponiendo ideas filosóficas, se discutían y se criticaban en el contexto de una conversación o un debate en el que participaban dos o más personas. El primer grupo de escritos de Platón incluye 35 diálogos y 13 cartas. 

 Fuente: buscabiografias.com

China: piden no salir a la calle por aumento de contaminación en Pekín

Las autoridades de Pekín y alrededores sugirieron a los ciudadanos que no salgan a la calle, ante la nueva subida de la contaminación, que recuperó este martes sus peores niveles.

El esmog causó el cierre de carreteras y la cancelación de vuelos para la semana de vacaciones que empieza el 9 de febrero en China.
El Centro Municipal de Supervisión del Medio Ambiente de Pekín mostró un índice grave de contaminación, mientras que la embajada estadounidense detectaba un nivel por encima del índice.

Fuente: bbc.co.uk

Científicos de EE.UU. logran penetrar un lago antártico

Un intento estadounidense de llegar a Whillans, un lago enterrado a una profundidad de casi 1 km bajo el hielo antártico, alcanzó su objetivo con éxito.

Los científicos informaron el domingo que los sensores de su sistema de perforación detectaron un cambio en la presión, indicando que habían hecho contacto con el lago.
Contenido relacionado

El proyecto Whillans hace parte de una serie de iniciativas emprendidas en los últimos años con el fin de investigar los lagos enterrados bajo la Antártida.

Una misión nada fácil. En diciembre, un equipo británico abandonó su proyecto de llegar al lago Ellsworth tras enfrentarse a dificultades técnicas.

Los rusos lograron obtener muestras de agua del lago Vostok, pero aún no han reportado algún descubrimiento relevante.

El lago Whillans está ubicado en el oeste de la Antártida, al sureste del Mar de Ross.

Es un denso sistema de corrientes, casi como un delta, que abarca unos 60 kilómetros cuadrados. El cuerpo líquido es bastante superficial, es decir, está a pocos metros de profundidad.

--> El equipo de perforación ha estado utilizando un taladro de agua caliente para derretir un agujero de 30 cm de diámetro a través del hielo subyacente.

El plan, ahora que el agujero es seguro, es bajar las herramientas necesarias para obtener muestras y sensores para después estudiar el lago, sus propiedades y su entorno.

Algunas de las muestras serán evaluadas directamente en el sitio, mediante laboratorios temporales ubicados en la superficie del hielo, y otras serán entregadas a universidades asociadas para un análisis más riguroso.

Según el blog Wissard, el espesor del hielo subyacente es de 801m, cifra que concuerda con las estimaciones realizadas a partir imágenes sísmicas.

Universo subglacial

Hay más de 300 cuerpos de agua subterráneos identificados en el continente blanco.

Se mantienen en estado líquido gracias al calor geotérmico y la presión, y forman parte de una gran red hidrológica y dinámica ubicada bajo la capa de hielo.

Algunos de los lagos están conectados, e intercambian agua.

Otros pueden estar totalmente aislados, y el agua podría haberse estancado en esos lugares desde hace miles o millones de años, lo que significa que probablemente alberguen microorganismos desconocidos para la ciencia moderna.

La profundidad del lago Whillans no es tan grande como la de Vostok (4 km) o Ellsworth (3 km), y su agua se intercambia con frecuencia debido a las corrientes subyacentes.
De hecho, las mediciones por satélite han revelado que el lago se llena y se vacía constantemente.

Por qué es importante

El gran interés de los científicos por estudiar los sistemas hidrológicos subglaciales de la Antártida se debe en parte a que el agua líquida bajo la capa de hielo tiene una influencia directa en su movimiento (el hielo sobre el lago Whillans se mueve a unos 300 metros por año).

Esta información se debe tener en cuenta a la hora de diseñar medidas que ayuden a lidiar con los efectos del calentamiento global.

Explorar entornos subglaciales también puede proporcionarnos una idea del potencial de habitabilidad de algunas lunas en el Sistema Solar.

Europa, satélite de Júpiter, y Encelado, que orbita Saturno, tienen grandes volúmenes de agua líquida enterrados bajo sus cortezas congeladas.

Los astrobiólogos piensan que estas lunas pueden albergar microrganismos extraterrestres.

El doctor David Pearce, del proyecto británico Ellsworth, calificó el avance en el lago Whillans de "emocionante".

"Siempre he pensado que estos proyectos son muy complementarios", le dijo el investigador del British Antarctic Survey a la BBC.

"El proyecto de Ellsworth tuvo lugar en las montañas transantárticas, en el punto más alto. Vostok está ubicado en la Antártida Oriental, y el proyecto fue Whillans está hacia la costa en una región del delta. La unión de los tres proyectos resultará en una mayor comprensión de lo que sucediendo bajo el hielo", explicó.

"Tendremos que esperar a ver lo que encuentran en Whillans, pero no me sorprendería que se descubran organismos marinos o evidencias de incursión marina. Si Whillans está abierto al sistema marino, está abierto a la incursión", señaló.

Fuente: bbc.co.uk

EigenValores y EigenVectores

Bueno Lectores en esta ocasion vamos a aplicar un tema interesante en el Algebra Lineal.

Que es Eigenvalores y EigenVectores

Se presenta como una aplicacion de la solucion de sistemas de ecuaciones lineales con n icognitas expresadas como AX = λX donde λ es un escalar. Pueden tomar otras formas como λX - AX = 0 o (λI - A)X = 0. Si λI-A es invertible, entonces, para X no hay sino solucion trivial, pero si det(λI - A) =0 (Ecuacion Caracteristica), entonces, a los valores de λ se los llama eigenvalores de A y a las soluciones para X, eigenvectores de A. 

Ejemplo : Hallar los eigenvalores y los eigenvectores para A si el sistema es:

X1 + 3X2 = λX1

4X1 + 2X2 = λX2

Planteamos la Solucion

 Solucion

1. Con la ecuacion caracteristica, se hallan los eigenvalores:

 

Es decir, (λ+2)(λ-5) = 0  Entonces
λ = -2

λ = 5

Los eigenvectores se obtienen cuando en (λI - A)X = 0 se soluciona para X teniendo en cuenta que (λI - A) es no invertible y por tanto tendra soluciones no triviales.

Asi que obtenemos los siguiente:

Si λ = -2 Tendriamos la siguiente Solucion,

Entonces tenemos lo siguiente:

-3X1 - 3X2 = 0

-4X1 - 4X2 = 0

Entonces analizando podemos observar que las dos ecuaciones son equivalentes el sistema tiene infinitas soluciones de la forma ( -t , t) con t ∈ R y de la misma forma, si λ = 5 entonces las soluciones serian los pares (3t/4 , t ) con t ∈ R que son los eigenvectores.

Nota : La explicacion mas a fondo la realizaremos en Video.

 

 

Pitagoras (Biografia)

Pitágoras de Samos es uno de los hombres más famoso y enigmático de la antigüedad (ca. 580 a. C. – ca. 495 a. C.), se escribieron varias biografías pero se han perdido y es difícil separar en su biografía lo que es de histórico de lo legendario. Nació en la Isla de Samos, junto a Mileto, hijo de Menesarco rico comerciante.Fue un filosofo griego responsable por importantes progresos en Matemáticas, Astronomía y Música.Se pueden distinguir en su vida tres etapas de acuerdo con los viajes realizados: a la India es donde entró en contacto con los saberes matemáticos y religiosos ,a Egipto donde estudia Geometría y Astronomía y a Babilonia es donde aprendió la media aritmética, la geométrica y la armónica Al regresar a Samos y encontrarla dominada por los persas, decide emigrar al sur de Italia estableciéndose en Crotona una de las más florecientes colonias griegas, donde fundó la escuela pitagórica, primera escuela internado del mundo, que llegó a convertirse en una asociación parcialmente religiosa,científica y filosófica, apoyada en la creencia de la inmortalidad del alma, la doctrina de la reencarnación, la práctica de alimentación vegetariana y un sistema educativo basado en la gimnasia, las matemáticas y la música Comenzó a enseñar filosofía y matemáticas con tanto éxito que entre el auditorio contaba con personas de distintas clases sociales e incluso asistían mujeres, que infligían un reglamento que les prohibía asistir a reuniones públicas, entre ellas asistió Theano hija de Milo, posadero de Pitágoras,hermosa joven con la cual se casó y quien escribió una biografía de él y seperdió.Sus creencias religiosas, sociales, políticas y su sentido de superioridad ofenden a los nativos del puerto de Crotona y genera rebeliones durante las cuales incendian la casa donde reside y huye a Metaponto, sus habitantes transformaron la casa donde vivía en un santuario, que le fue mostrada a Cicerón. Según la tradición dirigió por separado cuatro grandes discursos por: a los jóvenes, al senado, a las mujeres y a los niños cuyo contenido era la armonía y la justicia y de aquí surgió un gran entusiasmo por su figura. Hacia el final de su vida, su influencia y la de la escuela creada se hace creciente. Murió a los 80 años

PRINCIPALES APORTACIONES A LAS MATEMÁTICAS

Las ideas y descubrimientos científicos de la escuela pitagórica han sido atribuidos tradicionalmente a su fundador, Pitágoras, por lo que no se sabe exactamente cuáles fueron suyos y cuales de sus discípulos
•Invención de la tabla de multiplicar
•Demostración del teorema que lleva su nombre
•Construcción del pentágono regular y los cinco poliedros regulares
•Descubrió la existencia de los números irracionales
•Descubrió en geometría proporciones tan perfectas que las pensaba divinas sin sospechar que estaban estrechamente ligadas a un número perteneciente al mismo grupo
 •Los pitagóricos fueron los primeros en establecer demostraciones matemáticas mediante razonamiento deductivo
•Formación de los números cuadrados partiendo de la unidad y agregando la serie ascendente de los números impares
•Utilización de la palabra número solo para la suma de números enteros iguales
•Demostró que los intervalos entre notas musicales pueden ser representadas mediante razones de números enteros utilizando una especie de guitarra con una sola cuerda, llamada monocordio
•Descubrió la relación que existe entre la armonía de un intervalo de tono y las proporciones de las cuales producen dicho tono
•Afirmó " los números gobiernan el mundo
•Definió el infinito como " una cosa que no tiene magnitud asimilable"
•Algunos números los significaba como nefasto (13)
•Transformó el estudio de la Geometría en una enseñanza liberal
•Introdujo la demostración como recurso matemático.
•Clasificaron los números en pares, impares, perfectos, amigos,...
•Conocían la media aritmética, geométrica y armónica.
•Descubrieron la proporción musical: la media geométrica de dos números es la media geométrica de sus medias aritmética y armónica.
•Crearon el teorema que se refiere al llenado de un área con polígonos regulares.
•Son los creadores de 3 cuerpos platónicos: el cubo, el tetraedro y el dodecaedro

Fuente: es.scribd.com && wikipedia.org

Isaac Newton (1642-1747)

Newton disfrutó en vida la admiración y el respeto de sus contemporáneos. En el momento de su muerte Newton era presidente de la Real Sociedad de Londres y gozaba de la reputación de ser el más grande cient ífico de su época. Parte de la visión que tuvieron de él sus contemporáneos, es expresada en
el bien conocido epitafio de Alexander Pope: “Nature, and Nature’s Laws lay hid in Night. God said, Let Newton be! and All was Light”. En 1727 Isaac Newton fue sepultado en la abadía de Westminster, un honor que no había tenido ningún hombre de ciencia hasta el momento.

Se podría decir, en pocas palabras, que el logro de Newton fue expresar en leyes matemát icas el comportamiento de los cuerpos celestes y terrest res. La física newtoniana ofrecería la explicación más completa y armoniosa de la est ructura y movimiento del universo. Su obra mas conocida, los Prinicipios matemát icos de filosofía natural, se convirt ió en el sistema cosmológico de mayor reconocimiento desde Aristóteles. Newton sería entonces el más importante representante de la nueva física y de la ciencia
moderna, en donde tanto las matemát icas como la experimentación son aspectos fundamentales del método científico que, a diferencia de la filosofía aristotélica, no pretende explicar la causa del movimiento sino describir y predecir el comportamiento de la naturaleza a través de las matemáticas.

Fuente: uniandes

Biología cuántica: un mundo por descubrir

Desaparecer en algún lugar y reaparecer en otro. Estar en dos sitios a la vez. Transmitir información a una mayor velocidad que la de la luz.

Son fenómenos que se explican –desde hace un tiempo– a partir de la rama de la física que estudia el comportamiento de la materia y de la energía: la mecánica cuántica.


Sigue siendo una disciplina tentativa, incluso especulativa, pero de continuar creciendo, podría revolucionar el desarrollo de nuevos medicamentos, computadoras y perfumes, o incluso contribuir a la lucha contra el cáncer.
Hasta hace poco tiempo, la idea de que la biología -una ciencia que a los ojos de los físicos es cálida, húmeda y desordenada- estuviera relacionada con los estados de la materia se consideraba una insensatez.
Pero poco a poco y usando la poca evidencia que se ha ido encontrando, la idea ha empezado a cobrar importancia, explicó Luca Turín, del Instituto Fleming en Grecia.

Plantas, aves y narices

"Básicamente hay tres áreas en las que empieza a ser evidente la presencia de la cuántica, tres fenómenos que han derribado la idea de que la mecánica cuántica no tiene nada que ver con la biología", le dijo Turín a la BBC.

La más evidente de las tres es la fotosíntesis, el eficiente proceso mediante el cual las plantas y algunas bacterias construyen las moléculas que necesitan, utilizando energía de la luz solar.
Cuando se observa el proceso de cerca pareciera que hubiera pequeños paquetes de energía al mismo tiempo, "probando" todos los caminos posibles para llegar a donde necesitan ir para después escoger el más eficiente.
"La biología parece haber sido capaz de utilizar este tipo de efecto en un ambiente cálido y húmedo, manteniendo la superposición. No logramos entender cómo lo hace", le dijo Richard Cogdell, de la Universidad de Glasgow a la BBC.
La sorpresa no acaba ahí. Se cree que trucos similares pueden encontrarse en el comportamiento animal: las hazañas de las aves que cruzan países, e incluso continentes volando de polo a polo en sus rutas migratorias, podrían tener relación con la física cuántica.
Los experimentos biológicos muestran que, al migrar, los petirrojos sólo se orientan a través de los colores de la luz, y que basta con una radiofrecuencia débil para confundir su sentido de dirección.
Pero las explicaciones dadas no alcanzan a explicar el fenómeno.
Para los defensores de la relación entre la cuántica y la biología, la orientación de los petirrojos al migrar se debe a un efecto de entrelazamiento cuántico.
Según este fenómeno físico, las partículas entrelazadas (en su término técnico en inglés: entangled) no pueden definirse como partículas individuales, sino más bien como un sistema.
Por más distanciadas que estén dos partículas "entrelazadas", ambas saben lo que pasa con la otra, incluso parecen poder transmitirse información a mayor rapidez que la velocidad de la luz.
Los experimentos sugieren que este fenómeno ocurre dentro de las moléculas individuales de los ojos de las aves.
John Morton, del University College London, explicó que la manera en que las aves lo perciben puede parecer aún más extraño.
"Podríamos imaginarnos que es una especie de pantalla de visualización frontal, parecida a la que tienen los pilotos: una imagen del campo magnético impresa sobre todo lo que ven a su alrededor ", apuntó.

La idea sigue causando polémica. No menos la teoría según la cual que la biología cuántica la tenemos en nuestras propias narices.
La mayoría de los investigadores cree nuestro sentido del olfato depende únicamente de la forma que tienen las moléculas que aspiramos.
Pero el doctor Turín cree que, además de la forma, influyen las vibraciones de las moléculas, gracias a un efecto cuántico conocido como efecto túnel.
La idea sostiene que los electrones en los receptores de la nariz desaparecen en un lado de una molécula olfativa y reaparecen en el otro, dejando un poco de energía en el proceso.
Un artículo publicado en Plos One esta semana explica que las personas somos capaces de diferenciar dos moléculas de idéntica forma pero con diferentes vibraciones, lo que sugiere que la forma no es el único factor implicado en el proceso.
Lo que intriga a los investigadores es el alcance que puede tener la cuántica en los fenómenos de la naturaleza.
"No sabemos si estas tres áreas nos están introduciendo a todo un mundo por descubrir, o si realmente no hay nada debajo" –afirmó el doctor Turín. "No lo sabremos hasta que lo veamos"

'Sumamente Importante'

Este tipo de fenómeno ha suscitado un gran interés a nivel global. En 2012, la Fundación Europea de la Ciencia puso en marcha su programa Farquest, con el objetivo de crear una estructura de investigación cuántica a nivel europeo en la que la biología cuántica juega un papel muy importante.
Por otra parte, la Agencia de proyectos de investigación avanzados del departamento de Defensa de Estados Unidos (Darpa), estableció una red nacional de biología cuántica en 2010, y departamentos dedicados al tema están surgiendo en una gran cantidad de países que van desde Alemania a India.
Una mejor comprensión del olfato podría impulsar enormemente el negocio de la perfumería, con la creación de fragancias más personalizadas.
De igual manera, entender los trucos de la naturaleza podría contribuir al desarrollo de la próxima generación de computadoras cuánticas.

Pero el estudio de la biología cuántica puede tener repercusiones todavía mucho más profundas.
Ave reflejada en el agua

Simon Gane, un investigador del Royal National Throat, Nose and Ear Hospitaly autor principal del artículo publicado en Plos One, explicó que los pequeños receptores de nuestra nariz se conocen comúnmente como receptores acoplados a proteínas G.

"Son una subfamilia de los receptores que tenemos en todas las células de nuestro cuerpo, hacen parte de los retos implicados en el desarrollo de nuevas medicinas", explicó.

"¿Qué pasa si existe una interacción receptor-droga que simplemente no estamos notando por no pensar que se puede tratar de un efecto cuántico? Un descubrimiento semejante podría tener profundas implicaciones en el desarrollo, la creación y el descubrimiento de fármacos".

Jim Al-Khalili, de la Universidad de Surrey, está investigando la posibilidad de que el efecto túnel se produzca durante mutaciones en nuestro ADN - una pregunta que puede ser relevante para comprender la evolución de la vida misma, o para la lucha contra el cáncer.

Como le dijo el científico le dijo a la BBC: "si descubrimos que el efecto túnel está presente en las mutaciones, existe la posibilidad de que la física cuántica pueda explicar por qué una célula se vuelve cancerosa.

"Este sinfín de opciones -añadió- te hace pensar en la posibilidad de que la física cuántica no sea únicamente nuestra pesadilla de secundaria, o un campo de estudio alternativo liderado por un grupo de personas con ideas estrafalarias. Si realmente puede ayudar a responder algunas de las preguntas más importantes de la naturaleza, se convertiría en una ciencia sumamente importante".

Fuente: bbc.co.uk

Suspenden uso de resonancias magnéticas tras muerte de pacientes en Brasil

Las autoridades sanitarias de la ciudad brasileña de Campinas suspendieron el uso de imágenes por resonancia magnética (IRM) tras la muerte de tres pacientes poco después de haber sido sometidos a pruebas rutinarias.

No están claras las causas de las muertes. Las imágenes de resonancia magnética muestran los órganos internos del cuerpo, lo que permite a los médicos diagnosticar y tratar un gran número de enfermedades. Es además una técnica muy extendida.

 

Las imágenes de resonancia magnética muestran los órganos internos del cuerpo.

Fuente: bbc.co.uk

Ejercicios de Cantidades Positivas y Negativas

En esta oportunidad realizaremos el ejercicio numero 2 de la pagina 11 del Álgebra de Baldor. En el post anterior les deje una Recta numérica para que se ayuden si lo requieren si no la encuentran o no saben que es una recta numérica pueden entrar aquí para darles una explicacion mas profunda. Una vez dicho esto manos a la obra.

Ejercicio 2 "Cantidades Positivas y Negativas" pag 11 Álgebra de Baldor

1. A las 9a.m. el termómetro marca  +12° y de esta hora a las 9p.m. ha bajado 15°. expresar la temperatura a las 8p.m.

Solución

  a las  9a.m. marca  --->  +12°
  y de las 9a.m. a las 8p.m. ha bajado ---> 15°


 Por lo cual restaremos 15° a nuestra primera marca  +12°  teniendo así el siguiente procedimiento

            +12° - 15° =  -3°      Rta// -3°
 

2. A las 6a.m. el termómetro marca -3°. A las 10a.m. la temperatura es 8° mas alta y desde esta hora a las 9p.m. ha bajado 6°. Expresar la temperatura a las 9p.m.

A las 6a.m. marca ---> -3°
A las 10a.m. marca ---> 8° mas q a las 6a.m.
Y desde las 10a.m. a las 9p.m. ha bajado ---> 6°

 Por lo cual agruparemos todos los datos de grados y a -3° le sumaremos 8° y por ultimo le restaremos 6°
teniendo el siguiente procedimiento

-3°+8°-6°=  -1°  Rta// -1°

3. A la 1p.m. el termómetro marca +15° y a las 10p.m. marca -3° . Cuantos grados ha bajado la temperatura?

A la 1p.m marca ---> +15°
A las 10p.m. marca ---> -3°

Teniendo el siguiente procedimiento

+15°-3°= 12° Rta// Ha bajado 12°

4. A las 3a.m el termómetro marca -8° y al medio día +5°. Cuantos grados ha subido la temperatura?

A las 3a.m. marca--> -8°
Medio día = 12pm. marca ---> +5°

teniendo el siguiente procedimiento

-8°+5°=

5. A las 8a.m marca -4°; a las 9am ha subido 7°; a las 4p.m. ha subido 2° mas y  a las 11p.m. ha bajado 11°. Expresar la temperatura a las 11p.m.

A Las 8a.m. marca ---> -4°
A las 9a.m. subió --->7°
A las 4p.m subió --->2°
A las 11p.m. bajo ---> 11°

Teniendo el siguiente procedimiento

-4°+7°+2°-11°= -9°    Rta:// La temperatura a las 11p.m. es -9°

6. A las 6a.m. el termómetro marca -8°. de las 6a.m a las 11.a.m sube a razón de 4° por hora. expresar la temperatura a las 7am a las 8am y a las 11am.

A las 6a.m.  ---> -8°
De las 6a.m a las 11a.m sube --->4° por hora

Teniendo el siguiente procesdimiento

-8° + 4° = -4° ----> 7a.m.
-4+4°= 0° ---> 8a.m.
0°+4°= 4° --->9a.m.
4°+4°= 8° --->10a.m.
8°+4° = 12° ---> 11a.m.      Rta// La temperatura a las 7a.m. es -4°, a las 8a.m. 0° y a las 11a.m. 12°

7. A las 8a.m. el termómetro marca -1° de las 8 a.m. a las 11a.m. baja a razón de 2° por hora y de 11a.m a 2p.m. sube a razón de 3° por hora. Expresar la temperatura a las 10am. 11am 12am y a las 2pm

A las 8a.m. marca ---> -1°
De las 8a.m.a las 11a.m. baja a razón de ----> 2° por hora
De 11a.m. a 2p.m. sube a razón de ---->3° por hora

Teniendo el siguiente procedimiento

8a.m = 1° -2°(a las 9am -->-1°)-2°(a las 10am--> -3°)-2°(a las 11am-->-5°) = -5° a las 11a.m.
11a.m = -5°+3°(a las 12pm--> -2°)+3°(a la 1pm-->1°)+3°(a las 2pm-->4°)= 4° a las 2p.m

Rta// a las 10am= -3° , 11am= -5°, 12pm=-2°, 2pm=4°

8. El día 10 de dic un barco se haya a 56° al oeste del primer meridiano. Del día 10 al 18 recorre 7° hacia el este, expresar su longitud este día

Rta// -49

Espero les sirva en estos dias completo todo el ejercicio 2 saludos.

Matrices Para Resolver Ecuaciones Lineales

Matriz : Una Matriz es un arreglo rectangular de numeros

Matriz de coeficientes del sistema : Los coeficientes de las variables X1, X2.......Xn en un sistema lineal se pueden escribir como elementos de una Matriz A, llamada matriz de coeficientes del sistema.

Matriz Aumentada del Sistema : Se denomina matriz aumentada al arreglo rectangular de numeros, que representa un sistema Lineal, en el cual se omiten los signos +, las letras Xi, y los signos = de las ecuaciones del sistema a resolver.

Vamos aclarar esta Teoria con el siguiente Ejemplo:

X1 + X2 + 2X3 = 9
2X1 + 4X2 - 3X3 = 1
3X1 + 6X2 - 5X3 = 0

Si llevamos este sistema lineal a Una Matriz de Coeficientes el Resultado es el Siguiente:

Matriz de Coeficientes

Imagen Realizada en Software Algebrator

Nota: Al escribir la Matriz aumentada las incognitas deben escribirse en el mismo orden en cada ecuacion

Operaciones Elementales en los Renglones

1. Intercambiar dos Renglones

2. Multiplicar un renglon por una constante diferente de cero

3. Sumar un Multiplo de un renglon a otro renglon

Reduccion Por Renglones

El proceso de aplicar operaciones elementales con renglones para simplificar una matriz aumentada se llama "reduccion de Renglones".

Equivalencia por Renglones

Una Matriz A es equivalente por renglones a una Matriz B, si la matriz A se puede transformar en la matriz B mediante operaciones con renglones.

Forma Escalonada o Reduccion de una Matriz

Una Matriz esta en forma escalonada reducida por renglones si tiene las siguientes Propiedades:

1. Si un renglon no consta completamente de ceros, entonces el primer numero diferente de cero en el renglon es un 1 y se denomina pivote.
2. Si hay renglones que constan completamente de ceros, se agrupan en la parte inferior de la Matriz.
3. En dos renglones consecutivos cualesquiera que no consten completamente de ceros, el 1 principal o pivote del renglon inferior aparece mas a la derecha que el 1 principal del renglon anterior.
4. Cada columna que contenga un 1 principal tiene ceros en todas las demas prosiciones.

Nota: Si una matriz cumple con las propiedades 1,2,3 pero no necesariamente con la 4 esta en forma escalonada. 

Explicacion de la Teoria realizaremos unos videos para aclarar mas el tema en profundidad.


 

Cuadraticas Completas

Lectores presento el 2 video tutorial de la solucion de Ejercicios de Cuadraticas de la Forma ax2 + bx + c =0 donde demuestro el proceso para tener en cuenta al momento de realizar este tipo de Ejercicio.

Bienvenidos

Cuadraticas Incompletas

Bienvenidos Lectores en esta ocasion presento en video la definicion y ejemplos de un tema interesante que nos han solicitado explicacion. Este Tema se va dividir en 2 ya que es procedimiento para cuadraticas incompletas y completas. Bueno esperamos les halla gustado el procedimiento y analisis para resolver estos casos.

Ejemplos de Probabilidad II

1. En una bolsa tenemos 5 bolas numeradas del 1 al 5, si sacamos 2 bolas de la bolsa, cual es la probabilidad de tener un 2 y un 3 si no devolvemos las bolas sacadas?  y cual si las devolvemos?

  sin devolución la probabilidad seria 1/5 que es la cantidad de bolas entre el valor que saca por el 1/4 que es el que ya se saco   
                                          1/5 * 1/4 = 1/20  y 1/20 es igual a 0.05

 Con devolución seria 1/5 por 1/5 
                                                            1/5 * 1/5 = 7/25 y 1/25 es igual a 0.04


2. En una bolsa tenemos 7 bolas rojas, 9 bolas azules y 4 verdes, extraemos 1 bola calcula la probabilidad de que no sea roja
            
    Solución          

Explicacion: tenemos 7 bolas rojas y 9 bolas azules y 4 bolas verdes para un total de 20 bolas, entonces retiramos las 7 bolas rojas y nos quedan 13 bolas entre 9 azules y 4 verdes entonces la probabilidad seria de 13 bolas de cualquier color sobre la cantidad de bolas que en este caso serian 20

13/20 es igual a 0.65

3. Si lanzamos un dado mil veces, cuantas veces tenemos la probabilidad de que salga el resultado aproximada mente

Nos dan las siguientes probabilidades

  Probabilidad que saliera 1 = 0.05
  Probabilidad que saliera 2 = 0.2
  Probabilidad que saliera 3 = 0.4
  Probabilidad que saliera 4 = 0.15
  Probabilidad que saliera 5 = 0. 15
  Probabilidad que saliera 6 = 0.05


Solución

Aquí multiplicaremos la probabilidad que nos dieron de cada uno de los dados por la cantidad de lanzamientos entonces

  Probabilidad que saliera 1 = 0.05 * 1000 = 50
  Probabilidad que saliera 2 = 0.2 * 1000 = 200
  Probabilidad que saliera 3 = 0.4 * 1000 = 400
  Probabilidad que saliera 4 = 0.15 * 1000 = 150
  Probabilidad que saliera 5 = 0. 15 * 1000 = 150
  Probabilidad que saliera 6 = 0.05 * 1000 = 50

Entonces la probabilidad de q salga  1 es 50 veces , 2 es 200 veces, 3 es 400 veces , 4 es 150 veces,
5 es 150 veces y 6 es 50 veces.

si todo esta bien la suma de las veces tienen que darnos 1000

50+200+400+150+150+50 = 1000 ---> Correcto

Ejemplo de Probabilidad

1. Al tirar un dado consideramos los sucesos
    a =  par,    b = Mayor que 3,    c =  impar
    De los tres pares de sucesos posibles ab, ac y bc indican cuales son compatibles e incompatibles.

    Solución

• ab es compatible cuando salga el numero 4 y el 6 en el dado, porque se esta cumpliendo el suceso que dice la pregunta que si a es par b tiene que ser mayor que 3.
  y son incompatibles cuando se lanza y cae el numero 2 ya que Si yo saco el numero 2 estoy negando la afirmacion del suceso, por que 2 no es mayor que 3 con esto diríamos que no es compatible.
• ac  es incompatible la razón es si yo lanzo el dado y sale par entonces no puede ser impar y si hacemos lo contrario y sale impar no puede ser par
• bc es compatible cuando salga el valor numero 5 porque se cumple el suceso de ser impar y mayor que 3 y seria incompatible si cae en el 1 ya q no seria mayor que tres pero seria impar y si cae en 3 cumpliria ser impar pero no seria mayor que tres

Sistemas de Ecuaciones Lineales

Se llama ecuación lineal a una ecuación que solo tiene una única solución su soluciones son pares ordenados de números tiene infinita soluciones que se obtienen despejando una variable y dando valores cualesquiera a la otra.

Ejemplo 1 Problema explicación ecuación lineal

Un estante Contiene 3/5 de la cantidad total de libros que están en el estante vecino, si pasamos 10 libros del primero al segundo estante este tendrá el doble de libros que el primero. Cuantos libros había en cada librero?

x= Cantidad de libros

2(3/5x -10) ---> Primera ecuación
x+10 --->Segunda ecuación

x+10=2(3/5x-10)
x+10=6/5x-20
x=6/5-20-10
x-6/5x=-30
x-6/5X = -30
5-6/5 x = -30
-1/5x = -30
x= 150

Reemplazamos x que es igual a 150

3/5x150= 90

Rta// En el primer estante hay 90 libros y en el segundo150 libros

Ejemplo 2 Problema explicación ecuación lineal

1. x+3y-z=4
2. -2x+y+3z=9
3. 4x+2y+z=11

-2x+y+3z=9 -->Esta ecuación la multiplicaremos por 2 para hacer la reducción con la ecuación 3
4x+2y+z=11
----------------
-4x+2y+6z=18   --->Se cancelan las variables x
4x+2y+z=11
----------------
   4y+7z=29   --->ecuación 3

Ahora haremos la reducción de la ecuación 2

 x+3y-z=4  ----->Esta ecuación la multiplicaremos por 2 para hacer la reducción de la ecuación 2

-2x+y+3z=9
--------------
2x+6y-2z=8  ---->Se cancelan las variables x
-2x+y+3z=9
---------------
   7y+z=17   ----> Ecuación 2

Ahora multiplicaremos la ecuación 2 por -4/7 y la sumamos a la ecuación 3 para eliminar la variable y de la ecuación 3.

-4/7(7y+z=17) = -4y-4/7z=-4/7*17 y a esto le sumamos la caución 3

-4/7(7y+z=17) = -4y-4/7z=-4/7*17
   4y+7z=29

45/7z-135/7
45/7z = 135/7 ---> como es una igualdad los 7 se cancelan
45z=135
z=135/45
z=3

7y+z=17 ---> reemplazamos z que es igual a 3

7y+3=17
7y=14
y=14/7
y=2  

4x+2y+z=11 ---> ya podemos hallar x

4x+2*2+3=11
4x+4+3=11
4x+7=11

4x=4
x=1

Rta//  x=1, y=2, z=3

Bueno espero les halla gustado y nos leemos en una próxima oportunidad

Daniel Barragan

Fuente Definición : Notas de clase Álgebra lineal Facultad Ingenierías

Cantidades Positivas y Negativas

Cuando se estudian las cantidades pueden tomarse dos sentidos opuestos o que tienen condición de ser opuestos, se expresa el sentido de la cantidad mediante los signos + y -, anteponiendo el primero a las cantidades positivas, y el segundo a las negativas.

Generalmente, se designa al haber como cantidad positiva y a las deudas como negativa; a los grados sobre cero como positiva y a los grados bajo cero como negativa; el camino recorrido hacia la derecha o hacia arriba como positiva, mientras que hacia abajo o la izquierda es negativo; la latitud norte y la longitud este son positivas en tanto que la latitud sur y la longitud oeste son negativas; etc.

La fijación del sentido positivo en cantidades que puede tomarse en dos sentidos opuestos es arbitraria, es decir, puede tomarse a cualquiera de los dos sentidos como positivo; pero, una vez elegido, el negativo será el opuesto. Así, si en el segmento AB tomamos como sentido positivo de A hacia B, el sentido negativo será de B hacia A, y viceversa.

   El cero es la ausencia de cantidad. Es utilizado para expresar que una cantidad no es ni positiva ni negativa, pues el 0 es mayor que todas las cantidades negativas, pero menor que todas las cantidades positivas.

El valor absoluto de una cantidad es el número que representa la cantidad prescindiendo del signo o sentido de ésta y el valor relativo es el sentido de la cantidad. Puede considerarse al valor absoluto como al distancia de una cantidad al 0 en la recta numérica, por lo tanto, las cantidades positivas se hacen mayores a medida que su valor absoluto aumenta. En cambio, las cantidades negativas se hacen cada vez mayores a medida que su valor absoluto decrece.

Así, se diferencian dos tipos de cantidades: 

Cantidades aritméticas: son las que expresan solamente el valor absoluto de las cantidades representado por los números, pero no nos dice su sentido o valor relativo de las cantidades. 

 

Cantidades algebraicas: son las que expresan el valor absoluto de las cantidades así como su valor relativo o sentido por medio del signo.  

 

Una vez explicada la teoría podemos pasar a solucionar Ejercicios de practica a les dejare una imagen de una recta numérica que les sera muy útil en la solución de los ejercicios.

Tutoriales de Algebra de Baldor

Lectores hemos decidido hacer una serie de videos de solucion de la mayoria de ejercicios del algebra de baldor para que visualicen y asi puedan entender el desarrollo de los temas vinculados en este gran libro. Esperamos que les guste las clases virtuales.

Fuerza Magnetica

Sea n el número de partículas por unidad de volumen, v la velocidad media de dichas partículas, S la sección del haz y q la carga de cada partícula.

La carga Q que atraviesa la sección normal S en el tiempo t, es la contenida en un cilindro de sección S y longitud v·t.

Carga Q= (número de partículas por unidad de volumen n)·(carga de cada partícula q)· (volumen del cilindro Svt)

Q=n·qS·v·t
i=nqvS

Dividiendo Q entre el tiempo t obtenemos la intensidad de la corriente eléctrica.

La intensidad es el flujo de carga o la carga que atraviesa la sección normal S en la unidad de tiempo, que es el producto de los siguientes términos:

• Número de partículas por unidad de volumen, n
• La carga de cada partícula, q.
• El área de la sección normal, S
• La velocidad media de las partículas, v.

En el espectrómetro de masas o en el ciclotrón, ya hemos estudiado la fuerza que ejerce un campo magnético sobre un portador de carga y el movimiento que produce.

En la figura, se muestra la dirección y sentido de la fuerza que ejerce el campo magnético B sobre un portador de carga positivo q, que se mueve hacia la izquierda con velocidad v.

Calculemos la fuerza sobre todos los portadores (nSL) de carga contenidos en la longitud L del conductor.

El vector unitario u_t=v/v tiene la misma dirección y sentido que el vector velocidad, o el sentido en el que se mueven los portadores de carga positiva.

En el caso de que el conductor no sea rectilíneo, o el campo magnético no se constante, se ha de calcular la fuerza sobre un elemento de corriente dl

• Las componentes de dicha fuerza dF_x y dF_y
• Se ha de comprobar si hay simetría de modo que alguna de las componentes sea nula
• Finalmente, se calculará por integración las componentes de la fuerza total F

Fuente: shu.es

Experiencia Matematica

Buenos Dias Lectores 

En esta ocasion les voy a contar una experiencia sobre procesos para resolver los ejercicios al momento de Presentar un Examen:

1. Deben tener en cuenta el tema que les van a evaluar
2. Resolver Ejercicios Pero de Forma Matematica
3. Aplicar y leer los fundamentos y objetivos del Tema
4. Leer Muy bien el ejercicio y saber que le estan Pidiendo para resolverlo
5. Plantear las ecuaciones necesarias para resolver las incognitas
6. Mirar el sistema que se esta usando en el Ejercicio sea Sistema Ingles o Americano
7. Resolver
8. Revisar antes de entregar que todo este estipulado
9. Confianza en si mismo
10. Creer en lo que se ha realizado


Sigan esos 10 pasos y veran que el resultado de los examenes mejora ya que fue una metodologia que en primera instancia aplique para el rendimiento y el aprendizaje de la matematicas.

Saludos

Tutorial de Physion

Presentacion de un software Libre para realizar simulacion de Procesos Fisicos, Diseño de Mecanismos de 4 barras como tambien procedimientos alternos a movimiento vehicular.

Espero les Guste el proceso

Tutorial Algebrator

Bienvenidos Lectores en esta Ocasion Presento un software matematico para resolver ecuaciones algebraicas, sumas, restas, multiplicacion, esto es la presentacion del Software ire montando ejercicios realizados en el mismo con secuencia y analisis del caso.

Cordialmente

Cualquier inquietud sobre el software lo pueden verificar.

Movimiento Parabolico

Se denomina movimiento parabólico al realizado por un objeto cuya trayectoria describe una parábola. Se corresponde con la trayectoria ideal de un proyectil que se mueve en un medio que no ofrece resistencia al avance y que está sujeto a un campo gravitatorio uniforme.

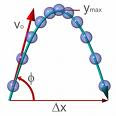
Puede ser analizado como la composición de dos movimientos rectilíneos: un movimiento rectilíneo uniforme horizontal y un movimiento rectilíneo uniformemente acelerado vertical

OBJETIVOS

1. Estudiar los conceptos básicos del movimiento parabólico descrito en la experiencia realizada en el laboratorio.

2. Describir las características del movimiento parabólico que realiza el balín.

3. Desarrollar los conceptos de velocidad, distancia y gravedad descritos por el movimiento y la distancia del balín al ser lanzados hacia distancias cada vez mayores.

4. Analizar por medio de los datos el movimiento y determinar su comportamiento con respecto al plano coordenado (abscisa x, ordenada y)

Tipos de movimiento parabólico

Movimiento de media parábola
El movimiento de media parábola o semiparabólico (lanzamiento horizontal)se puede considerar como la composición de un avance horizontal rectilíneo uniforme y la caída libre

Movimiento de media parábola

El movimiento parabólico completopuede considerar como la composición de un avance horizontal rectilíneo uniforme y un lanzamiento vertical hacia arriba, que es un movimiento rectilíneo uniformemente acelerado hacia abajo (MRUA) por la acción de la gravedad.

En condiciones ideales de resistencia al avance nulo y campo gravitatorio uniforme, lo anterior implica que:
1. Un cuerpo que se deja caer libremente y otro que es lanzado horizontalmente desde la misma altura tardan lo mismo en llegar al suelo.
2. La independencia de la masa en la caída libre y el lanzamiento vertical es igual de válida en los movimientos parabólicos.
3. Un cuerpo lanzado verticalmente hacia arriba y otro parabólicamente completo que alcance la misma altura tarda lo mismo en caer.

Ecuaciones del movimiento parabólico
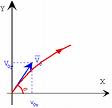
Hay dos ecuaciones que rigen el movimiento parabólico:

1. 
2. 

donde:

es el módulo de la velocidad inicial.

es el ángulo de la velocidad inicial sobre la horizontal.

es la aceleración de la gravedad.

La velocidad inicial se compone de dos partes:

que se denomina componente horizontal de la velocidad inicial.

En lo sucesivo

que se denomina componente vertical de la velocidad inicial.

En lo sucesivo

La velocidad inicial se compone de dos partes:

que se denomina componente horizontal de la velocidad inicial.

En lo sucesivo

que se denomina componente vertical de la velocidad inicial.

En lo sucesivo

Será la que se utilice, excepto en los casos en los que deba tenerse en cuenta el áng ulo de la velocidad inicial.
Ecuación de la aceleración

La única aceleración que interviene en este movimiento es la de la gravedad, que corresponde a la ecuación:

que es vertical y hacia abajo.

Ecuación de la velocidad

La velocidad de un cuerpo que sigue una trayectoria parabólica se puede obtener integrando la siguiente ecuación:

La integración es muy sencilla por tratarse de una ecuación diferencial de primer orden y el resultado final es:

Cuando un objeto es lanzado con cierta inclinación respecto a la horizontal y bajo la acción solamente de la fuerza gravitatoria su trayectoria se mantiene en el plano vertical y es parabólica.

 

Fuente: Libro Serway, Fisica Moderna